无梁楼盖的设计及构造要点(二)
无梁楼盖的配筋构造
文/曾朝杰、杜旭、卞海涛
昨天发布了无梁楼盖的节点形式与抗弯计算理论,主要包括无梁楼盖的柱帽形式及抗冲切计算,抗弯计算理论等内容,点击此处查看相应内容。今天推出无梁楼盖的配筋构造,包括框架柱的确定及柱顶、柱帽构造,抗弯配筋计算及构造。
// 框架柱的确定及柱顶、柱帽构造
1、无梁楼盖中间标准跨的框架柱一般是构造配筋,因此截面不宜过大,截面越大配筋越大,框架柱的截面由轴压比控制,注意当采用PKPM-SATWE计算框架柱轴压比时应该按照荷载规范的规定进行折减,多数情况下该处需要手动调整,程序不一定能完全计算准确。
2、对于左右不等跨或是与距边第二跨的柱子,以及左右两侧荷载不均匀而柱子承担部分的不平衡弯矩的情况,柱子的配筋可能较大,此时可以根据计算进行配筋,也可以在柱顶按照铰接考虑,使得框架柱不承受支座处的不平衡弯矩,而由左右两侧的板带弯矩自平衡,而计算时就需要把柱顶设置为铰接。柱顶铰接的构造图如图1所示。
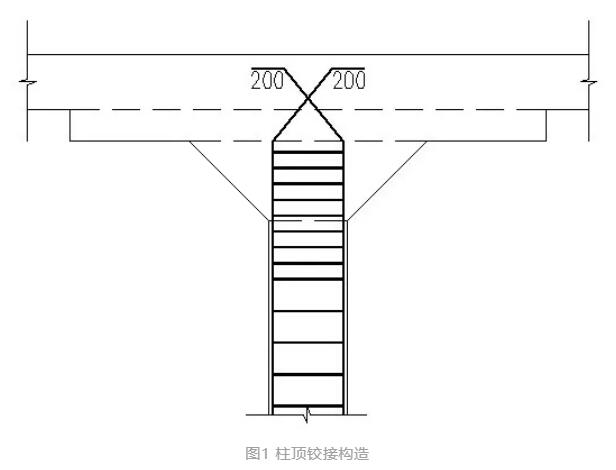
图1 柱顶铰接构造
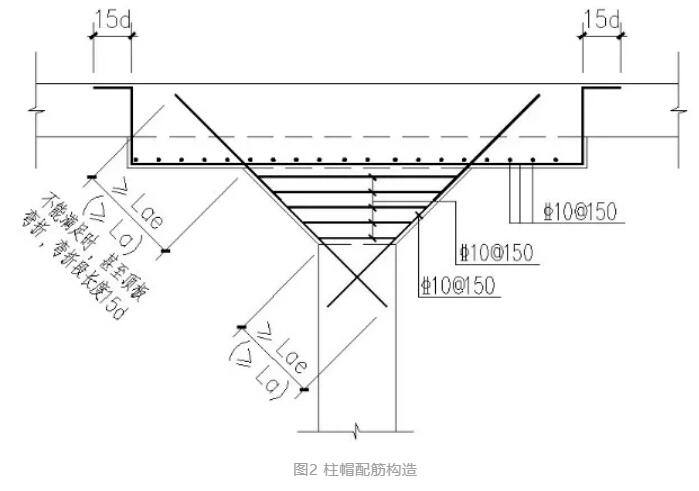
图2 柱帽配筋构造
3、关于带托板柱帽的配筋构造,包括两个方面:托板及台锥形部分,托板部分一般配置8~10,间距100~150mm的双向钢筋;台锥形部分是否需要配筋不同参考资料多有分歧,同济大学教材《混凝土结构基本原理》及《全国民用建筑工程设计技术措施》(结构-混凝土结构2003)对该部分不配筋,因台锥形部分属于刚性受压区范围,可以不配筋。而图集《11G101-1》中对板柱节点则有配筋要求,对该部分进行配筋是基于抗震的考虑。对于工程设计,用于抗震设计的台锥形部分需要配筋,非抗震时该部分可以不配筋,纯地下车库可以不配筋。但建议该部分配筋,主要是该部分配筋较小,同时配置钢筋也能增加受压混凝土的受力性能。构造如图2所示。
// 抗弯配筋计算及构造
1、抗弯配筋计算
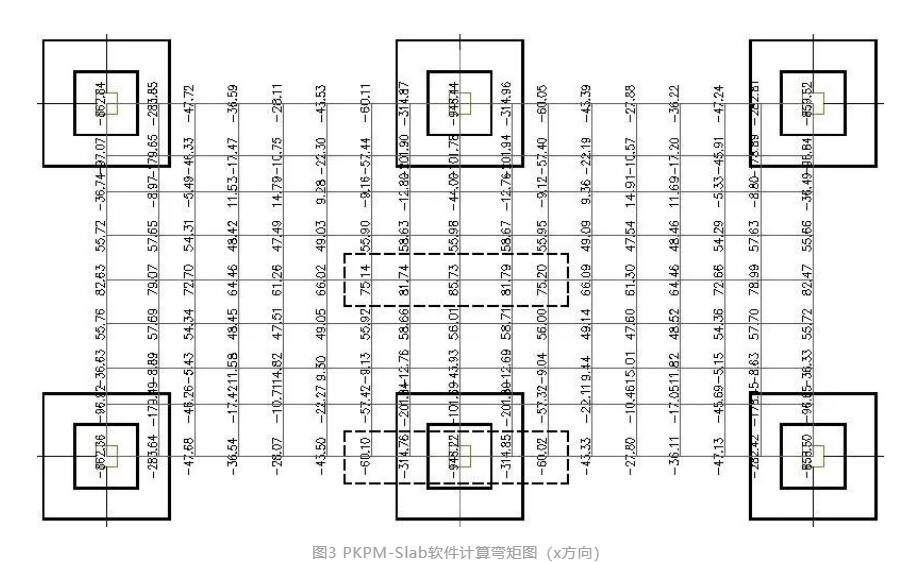
对于柱上板带的跨中部分、跨中板带的支座部分及跨中部分的配筋,按照板带梁的概念进行配筋,梁宽为板带宽度,也即1/2相应计算方向柱网的尺寸,梁高为板厚,设计弯矩值可以按照经验系数法里面的板带相应部分总弯矩,如果采用SLABCAD的电算结果,严格意义上应该采用相应断面的弯矩积分值,一般实际应用就采用计算点的加权平均值,如图3所示,图3为X方向的弯矩图:
图3 PKPM-Slab软件计算弯矩图(x方向)
由于计算机自动划分的网格线有时间距不均匀,但只要差别不大,这种差别可以忽略,认为网格间距基本相等,这一般也可以满足工程的精度要求。以柱上板带的跨中部分为例,柱上板带为图中虚线框所示,这时候柱上板带跨中部分的总弯矩可以通过简单的加权平均得到为:
再乘以板带的宽度可以得出柱上板带跨中部分的总弯矩,再根据矩形截面的算法计算配筋。
柱上板带支座部分的总弯矩值取值比较困难,因此,柱上板带总弯矩的确定最好是能结合经验系数法进行确定,由于柱上板带范围截面高度一般包括三个部分,纯顶板板厚部分,顶板加上托板板厚部分,顶板加上托板加上台锥形部分,如图4所示。
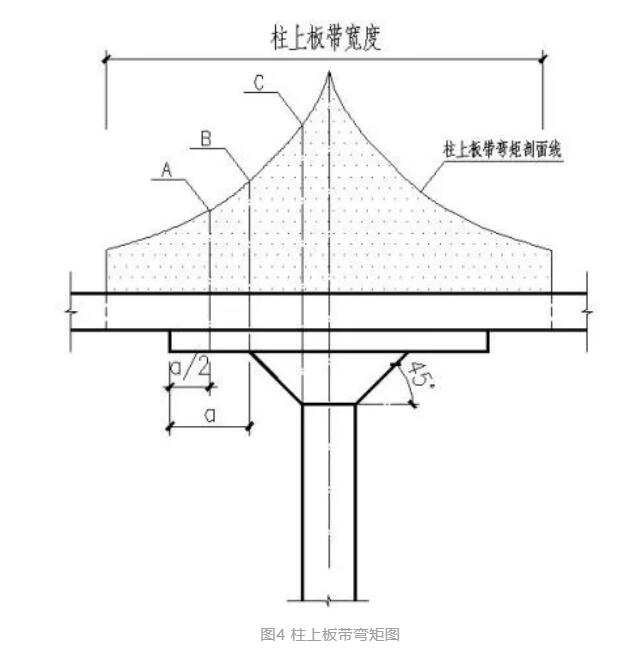
图4 柱上板带弯矩图
图中,柱上板带的配筋一致,如果B点的截面高度及配筋能抵抗该点的弯矩,则B~C段的材料抵抗图也基本可以包住弯矩图,C点至柱中心线的部分由于内力臂很大,所以配筋都能满足,则上图柱上板带弯矩可以简化为图5。

图5 柱上板带弯矩简化图
从上图可以看出,基本上A点的弯矩图就能代表柱上板带的弯矩平均值,A点的弯矩值乘以柱上板带的宽度就可以得到柱上板带支座的总弯矩,该总弯矩和采用经验系数法得出的柱上板带支座的总弯矩基本一致。
A点的弯矩如图11的-314kN/m2,再乘以柱上板带宽度则为柱上板带总弯矩。柱上板带支座弯矩的受力截面如图6所示,该截面为倒T型梁,受拉钢筋配置在顶面,也即倒T型梁的翼缘处,一般情况下,该截面的受压区高度小于腹板的净高h1,因此,可以直接采用截面宽度为B,高度为(h+h1)的矩形截面进行计算,计算得出的总配筋均匀布置在柱上板带宽度范围内即可。
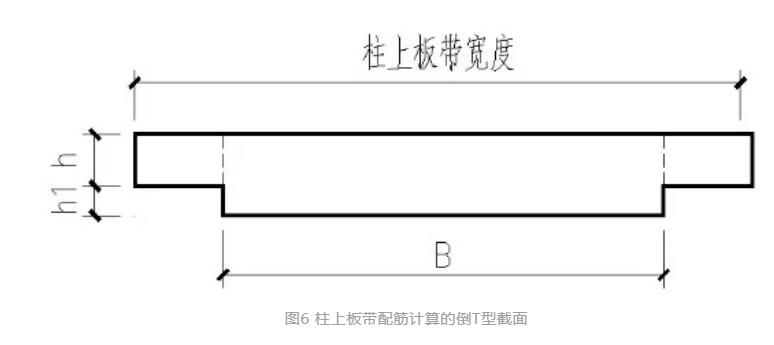
图6 柱上板带配筋计算的倒T型截面
2、抗弯配筋构造
由于柱上板带配筋一般较大,通常采用通长钢筋+附加钢筋的配筋方式,一般通长钢筋与附加钢筋配的量相等或接近,附加钢筋的截断点是关键,合理的钢筋截断点是根据弯矩包络图和抵抗弯矩图(材料图)来确定的。
柱上板带支座处附加钢筋的切断点,根据《混凝土结构设计规范》(GB 50010-2010)9.2.3条,对于板带受力构件,剪力一般都较小,不会配附加横向钢筋来辅助抗剪,所以一般情况下剪力V均小于0.7ftbh0时,当钢筋必须切断时,应延伸至按正截面受弯承载力计算不需要该钢筋截面以外不小于20d处截断,且从该钢筋强度充分利用截面伸出的长度不小于1.2La。根据规范,首先应先确定附加钢筋的不需要点,为了确定钢筋的不需要点,则先要确定柱上板带的反弯点。根据无梁楼盖弯矩系数法的内跨的弯矩系数,柱上板带支座弯矩系数为-0.50,跨中弯矩系数为0.18。根据材料力学,简支梁的截面弯矩方程为二次抛物线:
M(x)=-qx2/2+qlx/2
而对于受均布荷载且两端支座弯矩相同的梁,截面的弯矩方程为:
M(x)=-qx2/2+qlx/2+C
其中C则为两端支座弯矩。力学模型示意图为图7。
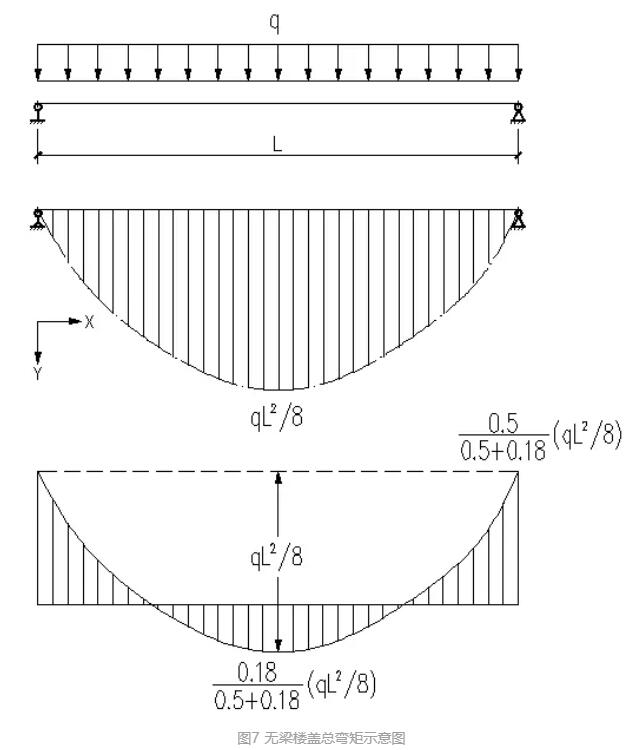
图7 无梁楼盖总弯矩示意图
根据上图,无梁楼盖柱上板带的弯矩方程为:
M(x)=-qx2/2+qlx/2-0.5ql2/(8×0.68)
令M(x)=0,即可以求得柱上板带的反弯点位置,为0.24L。
通过反弯点,可以确定柱上板带附加钢筋的不需要点,见图8。
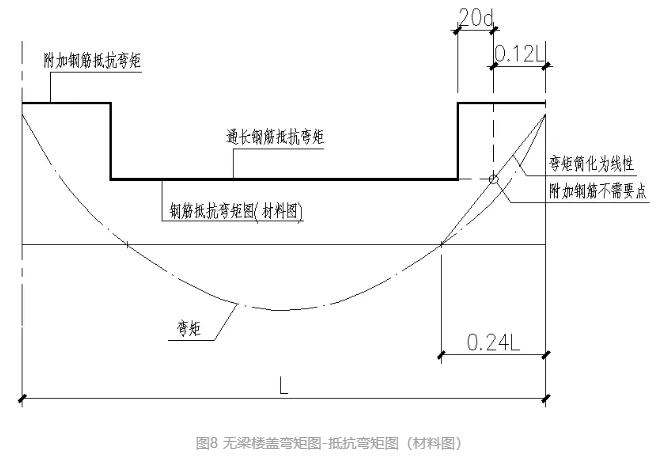
图8 无梁楼盖弯矩图-抵抗弯矩图(材料图)
支座处按照通长钢筋及附加钢筋各抵抗一半的弯矩,由上图可以得到附加钢筋的长度为:
0.12×L+20×d(15-7)
且根据上面计算的附加钢筋的长度宜大于托板的宽度B。由于支座处弯矩的二次变化简化为线性变化,使计算的结果偏于安全。
本文节选自《高层建筑基础分析与设计》,该书是国内大多数高校土建类专业高年级本科生、研究生教材,由同济大学梁发云教授与联境建筑曾朝杰、杜旭、卞海涛等合作完成,本书系统介绍了高层建筑基础的分析理论与设计方法,重视结合相关规范,强调对相关规范实质精神的理解和把握。包括高层建筑基础的特点和类型、地基勘察与地基模型、沉降计算理论、变刚度调平设计、(带裙房)高层建筑与地基基础共同作用分析及计算实例、高层建筑施工加载过程模拟分析,及高层建筑无梁楼盖设计等。知识体系系统,反映了本学科的前沿成果,使得本书既可作为高年级本科生教材,也可作为研究生或专业设计和研究人员的参考书籍。
现在该书已于8月23日由机械工业出版社出版,在京东、当当网上均可购买。

作者简介
曾朝杰,1989~1996期间在同济大学土木工程学院攻读学士和硕士,正高工,一级注册结构工程师,现任上海联境建设集团有限公司董事长、上海同建强华建筑设计有限公司技术负责人、担任同济大学校外研究生导师、上海市超限高层建筑抗震审查专家、《建筑结构》核心期刊审稿人、上海市房地产商会产业分会会长、上海楼宇科技研究会理事、四川商会常务副会长兼建筑建材专业委员会主任等职。主持住建部课题《无梁楼盖地下车库坍塌分析及设计施工风险控制关键技术》,主持研制上海市规范配套计算软件一部并成功应用于上海环球金融中心及上海中心大厦基础底板与桩基计算,主编上海市标准二部,参编四部国家行业及地方标准,并主编、参编多本著作与高校教材。
